[3D 打印建模] pyMins: 生成模型、加厚、封闭、输出stl

***软件采用python集成，功能丰富，集中前期多个算例；除非有对matlab等其他软件的特殊需求，建议考虑此版本***

2022.11.03提供下载地址：https://pan.baidu.com/s/1EsHiYZugi7WQ0tC3icRQKw  ；提取码：msib

0、讲个故事

前些日子跟大家分享了几个python或matlab代码，方便生成极小曲面并输出stl。今天跟大家分享个自己认为功能比较完整的软件。用python打包，直接运行的那种。主要特点有如下图：

大概就是说：

1. 包含三类曲面加厚方式，输出stl；
2. 包含三类坐标系；
3. 可以导入曲面再偏移加厚；
4. 当然可以实现梯度，只要给定合适的函数.

pyMins使用说明

1、 软件安装

pyMins为绿色免安装软件。下载压缩包，用WinRAR等解压软件解压（路径最好不含中文），找到pyMins.exe运行，弹出主界面，如图1所示。

图 1 pyMins主界面

2、 运行步骤

2.1 取值范围设置

首先根据需求在File- set range中设定x、y、z的取值范围及网格密度mesh density值，如图3所示。mesh density越大表示网格越细，曲面质量越好，但同时可能会影响曲面的生成速度。

图 3  变量取值范围及坐标系

2.2 isocaps生成实体模型

此方法主要用于隐式曲面，即形式为的曲面；坐标系可选择直角坐标、圆柱坐标及球坐标。

2.2.1 solid via end-caps

采用这类断面封闭方法，主要对曲面的各断面封闭处理，即通过填充 或 实现生成实体，如图4所示。

如果为常数，那么生成均匀的实体。

如果是变量x、y或z的函数，则生成具有一定梯度的实体。

.

图 4  solid via end-caps

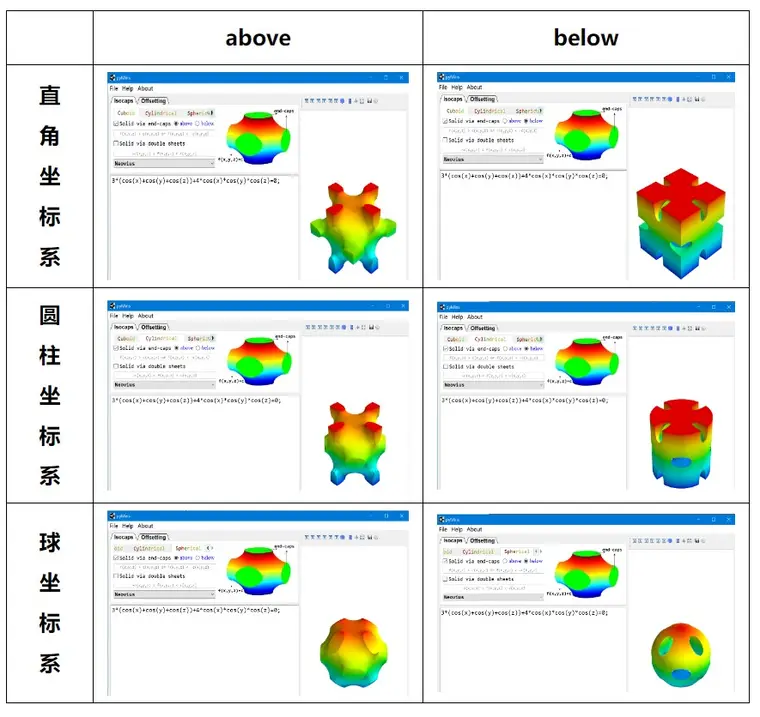
针对同一个曲面，不同坐标系下可通过改变填充方式生成6中各不相同的实体，如表1所示。

生成实体后，点击Save STL按钮将模型另存为stl格式。或点击预览区

图标另存为.jpg等其他格式，如图5所示。

图 5 模型另存为STL或其他格式

2.2.2 solid via double sheets

采用这类断面封闭方法，首先对曲面进行对称偏移，生成一个新的曲面，再通过填充之间的间隙生成实体模型，如图6所示。

如果为常数，那么生成均匀的实体。

如果是变量x、y或z的函数，则生成具有一定梯度的实体。

图 6  solid via double-sheets

在不同坐标系下生成实体及输出为stl或其他格式文件参考2.2.1。

2.3 offsetting生成实体模型

此方法仅适用于直角坐标系，可用于所有曲面（包括隐式和显示曲面）或用户导入的STL曲面文件，其中：

该方法此路如图7所示，即针对给定的曲面，沿每个顶点法向量偏移生成新的曲面，并填充这两个曲面的间隙从而生成实体模型。采用此方法生成一个厚度随z变化的圆柱体，即令，则生成的实体模型如图7所示。

图 7 solid via offsetting

输出为stl或其他格式文件参考2.2.1。

2.4 复杂实体模型

无论采用isocaps或offsetting法均可以生成复杂或梯度结构实体，为此只需将曲面表达式表示成复合函数即可。

若需将几种（或同种）极小曲面融合在一起，可采用以下连接函数构造

则可得到如下复合实体：

图 8 复合实体

例题2：梯度变化

为了得到梯度变化，只需中将设定为函数，如。

图 9 梯度变化实体

例题2：实体厚度随坐标变化

采用offsetting法，令，使显式曲面沿z方向厚度发生变化：

图 10 厚度随坐标变化

3、 符号说明

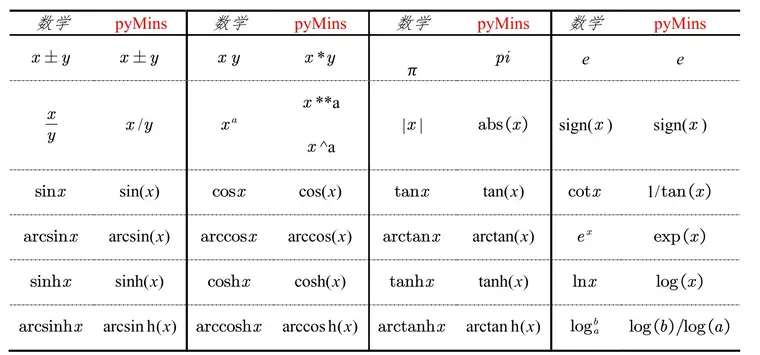
请联系QQ180280578、微信allisforA

下载地址：https://pan.baidu.com/s/1EsHiYZugi7WQ0tC3icRQKw  

提取码：msib